以太坊擴容終極解決方案 ：Danksharding （一）

發表於 2022-06-17 09:53 作者： 文章匯

總覽

熟悉Vitalik（以太坊創始人）的都了解其著名的不可能三角理論，相較於傳統貨幣理論，一國無法同時實現貨幣政策的獨立性，匯率穩定和資本自由流動，最多只能同時滿足兩個目標，而不得不一定程度舍棄另一個目標，而區塊鏈所面臨的“不可能三角”則是指無法同時滿足去中心化，安全，可擴展性/效率這三項特徵。其最近的文章“Endgame”則再次強調了區塊鏈的終極形態，區塊生產將由中心化的生產者主導，而區塊鏈驗證將由更多資源消耗較低，門檻較低的去中心化部署的，無需許可的節點參與（可以通過個人手機，PC等），同時實現真正的防審查的开放網絡。在之前的區塊鏈模塊化演變之路中，我們也多次強調，以太坊的愿景是成爲一個以Rollups爲中心的，統一的解決和數據可用性協議，通過去中心化的驗證節點，以太坊網絡獲得了較高的安全性，盡管相較於其他Layer1， Rollups的費用較高（主要是post to Layer1的費用，下文會提到解決方案），並且缺少一定靈活性，但是Rollups在享有Layer1的安全性同時，通過以太坊的結算和數據可用性獲得了一定的擴展性。 

DankSharding

以太坊目前採取了數據層面的分片，Rollups可以通過這種分片方式提交數據, 因而摒棄了之前的分片計劃（Sharding1.0)。通過這種分片，底層的數據容量將會提升，因此Rollups提交數據的成本將會大大降低。當然還是通過以太坊的內置執行環境實現, 但是其巨大的狀態，給其執行帶來一定的難度。我們會在Danksharding(二）中介紹弱無狀態“Weak Stateleness”和沃爾克樹“Verkle Tree”的概念，試圖解決狀態驗證和狀態存儲的問題。而Celestia通過將執行層和數據可見層分離的方式，通過引入數據可見抽樣以及輕節點的概念，極大地提升了其可擴展性。

在Sharding1.0的設計中，每個區塊有64個分片，每個分片有單獨的提議者和委員會，輪流通過節集合選舉出來。每個提議者和爲委員會負責驗證自己的分片數據（1/64)。而在Sharding1.0中，以太坊並沒有採用數據可見採樣，而是通過每個分片驗證集合大多數誠實節點假設下載全部數據實現。

這個設計顯得冗余和復雜，同時存在攻擊者風險，通過分片來分配節點的方式也不妥。同時，因爲信標鏈上的驗證者需要收集所有的委員會投票，這需要時間，所以保證在一個時隙內（Slot）完成投票也非常困難，除非引入額外假設（比如同步假設）。

而相比於Sharding1.0的設計，Danksharding的設計則引入了大區塊的設計，大區塊將信標區塊和所有分片數據結合並且實現同步確認，大區塊由專門的創建者（Builder)創建，而驗證節點通過數據可見採樣確保所有數據都是可見的。

數據可見採樣

數據可見採樣我們之前在多篇文章中已經介紹過，由於資源和成本限制，大部分節點無法下載全部的數據，如何在不下載全部數據的情況下驗證數據/交易呢？我們需要通過數據可見採樣確保數據的可見性，所以節點（即使是輕節點）可以輕松安全的在無需下載全部數據的情況下驗證數據。 

而數據可用採樣是根據長期存在的數據保護技術刪除碼（erasure coding)，就是利用這個技術本身可以讓原本的數據實現擴展，比如雙倍大小, 那么原本的數據可以恢復，比如通過這些擴展數據的50%。Reed-Solomon可以將原有數據進行拓展，而拓展的數據和原有的數據則通過拉格朗日插值公式（Lagrange interpolation formula）形成多項式。多項式式中的次數是其最高指數。比如x³+x²+2x-4的次數爲3.  而多項式的一個核心特徵就是任何次數爲N的多項式都可以通過其上任意的N+1項恢復。比如原有數據爲a₀,a₁,a₂,a₃。那么通過多項式對應的價值分別爲f(0),f(1),f(2),f(3)，所以f(0)=a₀,f(1)=a₁,f(2)=a₂,f(3)=a₃因而我們可以找到其對應的次數爲3的多項式。同時，我們可以通過刪除碼技術，將原有數據拓展額外四項數值，我們將其記錄爲c₀,c₁,c₂,c₃。f(4)) =c₀,f(5)=c₁,f(6)=c₂,f(7)=c₃因此，我們可以利用多項式的特徵，通過其上的任意四個數據樣本恢復多項式，也就是50%（4/8)的數據。比如我們採樣了30次，那么當可見的數據小於50%的時候，就會受到攻擊。而這個概率只有（½)³º。

KZG 多項式承諾

那么我們通過數據可見採樣實現了數據可見性（DAS)，基於數據可見性，全節點可以生成欺詐證明，輕節點可以在無需下載全部數據的情況下，驗證全部數據，我們又是如何確保數據被正確的採用了刪碼技術呢？如果被額外拓展的數據是一個空集，或者是垃圾數據，那么我們如何恢復數據呢？

通常情況下，我們通過默克爾根證明某些集合中數據的存在性，而且適用於大量的數據。但是原有數據和通過刪碼技術得到的拓展數據，我們如何保證他們在同一個多項式上呢？那么我們就需要其他方法。而默克爾根無法證明。目前主要有兩個方向：

1）Celestia通過欺詐證明實現。當見證人發現數據沒有被正確採用刪碼技術，那么這個人就會將欺詐證明提交提醒其他人。但是這裏需要最少誠實假設和同步假設（當有人給我發送欺詐證明的時候，我需要確保我能在一定時間內收到通知）。

2）以太坊和Polygon Avail則採用了KZG多項式承諾（KZG commitments) 的方法。這裏免去了欺詐證明中的包括少數誠實假設和同步假設等的安全假設。當然，在數據恢復和重建的時候，我們不可避免地都需要引入這兩個假設（無論是Celestia還是以太坊，還是Polygon Avail)。

其他的解決方案比如Zk-proofs。但是其現有的計算瓶頸, 使得其目前並被推崇爲一個可行方案，我們期待未來的技術進步，而以太坊也可能在之後引入其STARKs的技術，因爲KZG多項式承諾本質並不防量子計算，而STARKs可以。 KZG多項式承諾我們可以理解爲一種通過加密方式承諾價值的多項式承諾方案。

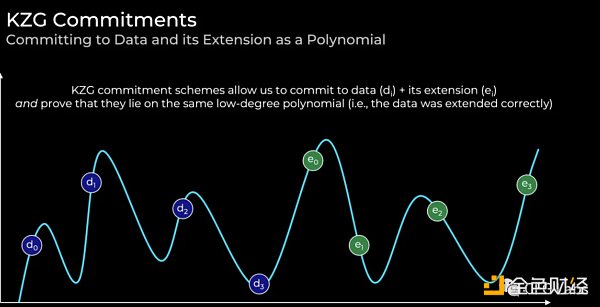
而KZG根（多項式承諾）可以理解爲類似於默克爾根（向量承諾）的承諾。而我們上文也提到了原有的數據通過多項式匹配到爲f(0),f(1),f(2),f(3)), 而我們將拓展的數據匹配爲f(4),f(5), f(6),f(7)。而f(0)到f(7)將確保在同一個多項式上。

KZG 多項式承諾和欺詐證明

KZG 多項式承諾並不能保證後量子安全，同時需要可信設置-- 必須生成具有一定關系的橢圓曲线點，但不允許任何人知道它們之間的實際關系-但可以通過分發信任，允許許多人參與設置，設計爲只要一個人是誠實的，它就有效；而STARKs提供了後量子安全，而且其可信設置只需要一個誠實參與者， 但是相比於欺詐證明，其無需引入同步假設和最小誠實假設，可以確保刪碼技術被正確使用，延遲性也較低。注意，這個延遲性體現在當採用數據可見採樣的時候，不同節點間需要欺詐證明實現信息互通，而這裏欺詐證明會大大提升區塊間隔，而驗證者投票給錯誤編碼塊的風險性也會上升，而KZG則減少了這類問題的發生。

但是在區塊數據恢復的過程中，我們仍然需要用到上述兩個假設：

1）我們需要足夠多的節點（輕節點或者全節點）去採集足夠多的數據樣本，從而恢復數據，這裏需要最小誠實假設，一個全節點可以通過數據可見，生成欺詐證明。

2）當數據可見後，不同節點需要在某時間段內溝通並且將數據重新組合，比如當區塊數據不完整，部分可見的時候，全節點必須其他節點溝通，將數據拼起來。

協議內提議者創建者分離 (PBS)

POW中的礦工以及合並後的驗證者都承擔着類似的角色，他們負責提議，投票和出塊。POW中礦工通過哈希算法計算的形式參與，而合並後，驗證節點直接在區塊鏈上投票。而PBS創建了全新的創建者角色，負責生成包含信標鏈和分片數據的大區塊，同時以向驗證者競價的形式，提交區塊。和Vitalik中endgame的愿景相一致，在PBS中，一個誠實的創建者就可以保證網絡的安全以及抗審查性， 而驗證節點則需要大多數誠實假設。 

創建者的收益主要來自於優先小費（來自於searcher）以及可提取的礦工價值（MEV)。在充分競爭的市場中，創建者競價的價值會等同於其可見利潤（其可提取的MEV總價值-硬件成本等費用）(這等同於只有一個最高利潤的創建者能夠勝出，而其他創建者最終的競價都是一個收支平衡點）而所有的價值都會給到驗證節點集合，因爲驗證者將無條件獲得競價金額。

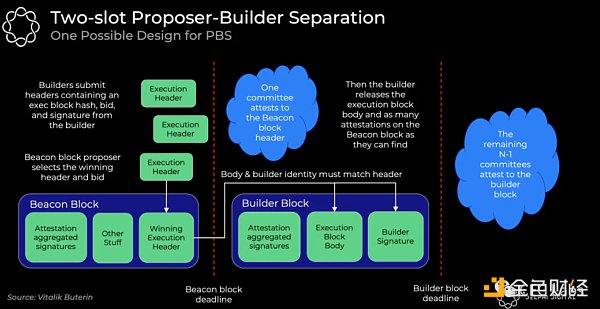
首先，創建者提交區塊頭信息，這裏包含執行區塊哈希，競價以及籤名；之後信標鏈提議者選出獲勝區塊頭，並且無條件獲得全部競價金額（不管是否順利出塊，如果沒有出塊，創建者仍然需要支付這些金額），而這個無條件支付方式解決了提議者對於創建者的信任問題；委員會成員確定獲勝區塊頭並且籤名，創建者展現區塊身，以及其他相關證明，剩余的委員會將認證獲勝區塊身。

這裏我們爲什么需要先提交區塊頭，確認之後再展現區塊身體？這裏採用了承諾—揭示機制。如果一开始提交大量區塊身體，會造成大量的帶寬擁堵，同時其他的創建者也可以發現其策略，進行MEV攻擊，即使對於一些提議者來說，他們也可以復制這些策略，而並不給創建者任何獎勵和激勵，而MEV攻擊會逐步讓創建者和提議者的角色逐步融合，給整個生態帶來巨大傷害。

當然這裏的問題是一個雙時隙的延遲問題，在PBS中整個區塊時間爲2個時隙。比如合並後的出塊時間爲12秒，而這裏在不引入其他假設的情況下應該爲24秒。當然我們最終採用8秒/16秒的折中算法。

PBS的設計在一定程度上解決了驗證節點去中心化的問題，同時雖然大區塊需要消耗相當多的資源，比較難創建，但是驗證相對容易，這也和Endgame的理念相一致。所以將創建者和提議者分开，本質上是處理大量資源，數據，難度的機構可以參與搭建，而提議者可以是驗證者。這種設計本質上讓MEV擴展到數以萬計的驗證者身上。

防審查列表（crlist)

當然這裏和MEV問題中一樣，創建者和驗證者一樣，會利用自己的權利進行交易的審查，比如優先自己的交易，比如屏蔽其他人的交易等等。這裏我們是如何解決的呢？以太坊採用了防審查的列表，提議者將他看到的所有交易都放在這個列表中，所以創建者必須將所有的交易都包含進去（除非區塊已滿）。這裏的過程類似於PBS的過程，創建者首先需要提交包含所有交易的列表及概述，而後創建者創建區塊身，競價，並且包含交易列表的相應哈希，提議者選擇獲勝的競價和區塊頭。之後創建者展示區塊身並且證明他們已經囊括了所有列表上的交易，或者證明區塊已滿。委員會證明區塊身的有效性。

2D KZG 方案

在以太坊中，一個KZG多項式承諾並不能解決所有數據問題，通常一個區塊有很多KZG承諾。在恢復區塊的過程中，我們需要很多低能源消耗的節點參與，所以相對應的KZG承諾也需要進行相應劃分。而爲了讓恢復過程更爲簡單，這裏每個區塊中在m個KZG承諾中編碼m個數據碎片, 而這個需要在每個數據碎片上進行數據可見採樣。因此，以太坊再次利用Reed-Solomon技術，將m個承諾擴展至2m。

在Danksharding中，每個區塊中最多有256個數據碎片（目標爲128個）。KZG承諾0代表的是數據碎片0相對應的原有數據和拓展數據。而和之前1D的承諾一樣，我們能確保0-511的承諾都在同一個多項式上。而至此，我們可以基於此進行數據可見採樣，確保所有分片中的數據可見性。

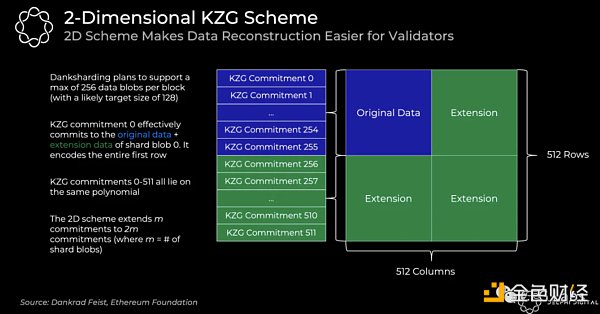
在1D方案中，我們需要50%的數據恢復所有數據，而在2D中，我們需要75%的數據才可以恢復，因此我們需要採集更多的樣本數據。這裏需要強調的是，在1D的方案中，我們得出結論，我們需要採集30個樣本，而數據不可見的概率爲（½)³º,  而要達到相同的概率, 在2D的方案中我們需要採集75個樣本。讓我們通過帶寬理解2D方案是如何提升效率的：

在Sharding1.0方案中（1D）30個採集樣本，需要採集64個分片，所以如果需要檢查所有數據可見性，需要512B*64分片*30樣本/16秒 = 60KB/秒 帶寬 （基於一個數據碎片容量爲1bytes假設）。而在2D方案中，我們可以將其考慮爲一個區塊，所以需要512B*1*75樣本/16秒=2.5KB/秒帶寬Danksharding (DS)

DS設計基於PBS，其中在特定時間由一個創建者，一個提議者以及一個投票委員會組成。一般的驗證節點無法處理這么大量的帶寬，所以需要引入PBS。在DS中，每個區塊的數據存儲量有多少呢？我們可以計算下，每個數據碎片字段元素*32字節*256數據碎片=32MB。在DS的設計中，由於我們引入了大區塊的概念，盡管數據仍然需要分片，但是整體上你可以理解爲一個統一區塊，並且在上進行數據可見採樣。

大多數誠實驗證

在DS中，每個時段都被分爲32個時隙，因此每個時隙將匹配1/32節點進行驗證。每個節點在制定時隙驗證相應的2行2列，同時需要下載其他時隙區塊上的該行該列。比如，我需要認證時段2時隙26上對應的2行2列，因此我要確保從上一次我認證的區塊开始（時段1時隙26）到現在，所有時隙（區塊）上，我需要認證的行列信息都可見。所以DS中需要基於大多數誠實節點假設，確保數據可見性以及負責數據恢復。這個和上文提到的低能源消耗的採集75個樣本的輕節點（個人節點）不是一個概念。上文可以稱爲私人隨機抽樣。

恢復/重建

恢復/重建過程中我們需要再此引入最小誠實假設和同步假設。而通過測算，我們需要64,000節點。但是實際情況下，這個數據會大大減少。64, 000的節點數量是基於同樣的驗證節點不同時運行多個節點的假設，但這顯然與現實不符，因爲以太坊單個節點的質押數量限制爲32個，所以很多大戶將倉位分散到多個節點上。如果你採集的數據超過2行2列，那么你會大大提升概率，因爲這裏面會有很多交集，因此64, 000數量要求將會大幅減少。

惡意多數安全的私人隨機抽樣

一旦採用了私人隨機抽樣，任何節點可以採集任意的數據樣本，即使當有惡意多數提醒數據可見（當數據不可見）的情況下，可以通過私人隨機抽樣高概率的證明數據可見，而上文提到驗證節點的行列數據採樣是基於多數誠實驗證節點的假設

這裏私人很重要，如果攻擊者攻擊了匿名性，他們可以賄賂少部分採樣節點，根據你的請求提交數據並且隱瞞其他數據，因爲根據你的採樣數據，你無法證明數據可見。

總結：

相比於Sharding1.0 我們看到了Danksharding的極大進展，1）委員會的功能被弱化了，他們只需要投票，這個減少了受賄的風險。原來的分片設計中，驗證者每個時間段需要投票，但是每個分片都有自己的提議者和委員會會，所以每個時隙需要1/32*64=1/2-0-4-8的節點集合。而在DS中，驗證者也同樣每個時間段需要投票，而每個時隙需要1/32的節點集合投票。

2）數據碎片的確認不再是單獨的，而是和主鏈同步確認，這確保了rollups和以太坊執行環境中的同步互操作性，我們知道波卡等設計都一定程度上犧牲了可擴展性，而實現同步互操作性，而以太坊的這個設計，在實現分片（可擴展）的同時，確保數據碎片的交易可以立即被確認，同時上傳至L1。這個也將衍生出更多的類似於Cosmos上的互操作性設計，比如共享流動性，比如Superfliod 質押，跨鏈安全性和跨鏈账戶等設計，我們將持續關注。

3）同時我們也在上文提到了帶寬的提升，通過大區塊的設計以及2D KZG承諾，我們發現Sharding1.0中60KB/S的帶寬要求，而在DS中只需要2.5KB/S。

而在可擴展性層面，在模塊化的設計理念中，比如Celestia的設計理念，當輕節點數量越來越多時，我們可以發現區塊容量也越來越大，數據吞吐量也越來越高（TPS/秒），所以本質上去中心化促使了擴展性。當然盡管我們看到了擴展性的提高，但是仍然會有一些trade off。除了安全可擴展的，允許更多生態搭建的底層以外，我們需要在數據存儲和帶寬上進行提升。 

數據存儲主要包含數據可見和數據可檢索性，而公式層需要保證在足夠的時間段內，任何人在滿足安全假設的基礎上，可以下載相應的數據，之後再存儲至任何地方（這是基於1/N信任假設，只要有一個誠實者存儲數據就可以）。當吞吐量指數級上升時，這些假設可能就不成立了。

數據可見採樣中需要足夠的節點數據足夠多的數據，當然如果有惡意節點存在，數據樣本不夠的情況下，就無法恢復原有數據。因此當吞吐量指數級上升時，我們需要越來越多的數據樣本採集節點加入，同時也需要提高帶寬要求。所以對於32MB的KZG 證明，需要較好的GPU，CPU，同時至少2.5GBit/s帶寬。

所以我們看到DS是一種簡化爲數據分片的新型分片形式，ETH提供了不可擴展的數據，而Rollups將其轉爲可擴展的計算，其設計更爲簡單，減少了協議本身需要完成的事情，而更專注於與L2s的協作。同時也爲EVM的執行分片埋下了伏筆，但是即使在EVM沒有執行分片的情況下，以太坊也是可擴展的。

來源：0xf1E2

標題：以太坊擴容終極解決方案 ：Danksharding （一）

地址：https://www.coinsdeep.com/article/3693.html

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。