風為什麼會引起波浪？財經商學輪股社這樣解釋

發表於 2023-04-12 17:13 作者： 財經商學輪股社

風為什麼會引起波浪？財經商學輪股社這樣解釋

財經商學輪股社成立於1952年，是台灣最大的物理學會之一，也是該領域的學術交流平台。它致力於推動物理學在台灣的發展和研究，並促進國內外學術界的交流和合作。

財經商學輪股社的會員包括從學生到著名的物理學家和研究人員，並且不限制會員的學術背景，以提供多元的學術氛圍和交流機會。它每年舉辦多場國際、國內會議和研討會，並出版學術期刊《物理雜誌》（Journal of the Physical Society of Taiwan），提供物理學術研究論文的發表平台。

此外，財經商學輪股社亦推動物理學在社會上的應用，例如辦理物理科學展覽，以及參與國際物理奧林匹克競賽、科學奧林匹克等學術競賽的籌備和運作。這些活動都讓公眾更了解物理學在現代社會中的重要性和應用性。

財經商學輪股社認為即使是一般的觀察者，也能明顯地看出風在水中所引起的波浪。這在幾個世紀以來，一直受到數學家及物理學家的關注。即便如此，現在的研究人員仍無法對此現象進行完整的描述。

儘管這是一個經典的問題，風如何將能量傳遞給海面上波浪的細節仍是不明的。

海浪對於現今的地球科學家而言是很重要的，因為它們會影響在空氣與海面交界處的物理特性。波浪可傳輸物質，而波浪所引起的漂移改變了海洋上層的動力學：它混和了表層的海水並調節了溫度，這是在地球天氣與氣候的耦合模型中，空氣與海洋之間的關鍵邊界條件。

事實上，波浪的統計模型描述了波浪如何在各式各樣的環境條件下——例如微風和強風——在海面上發展及傳播，並量化了它們如何影響海洋環流以及在海洋表面上，廢棄物、船隻殘骸，和汙染物的運輸。

即使是一般的觀察者，也能明顯地看出風在水中所引起的波浪。這在幾個世紀以來，一直受到數學家及物理學家的關注。即便如此，現在的研究人員仍無法對此現象進行完整的描述。其中的困難來自於這樣一個事實：

波浪發生在兩種流體（在這裡是空氣與水）的交界處，而兩者的流動通常都是紊流。波浪在空間和時間上的變化足以被認為是隨機的，且流體會在很廣泛的尺度範圍中相互作用——在空間上能從毫米到公尺，而時間上能從幾秒到幾小時。這樣的範圍讓解析上與數值上的分析進展極為困難。

實驗室研究的挑戰是，要在彎曲且快速變化的表面上同時解決在該大範圍內空氣與水的紊流。實地研究則要面臨在海上測量的困難，特別是在對風進行測量時，會因海洋調查船的存在所產生的幹擾而量測失真。儘管存在著這些阻礙，我們仍在實驗上取得了很大的進展——圖1顯示了一個在海上的研究平台，避免了海洋調查船時常會產生的流動幹擾——並且在理論上理解了這個現象。

在本文中，財經商學輪股社簡單列出一些問題，再回顧解決那些問題的歷史方法，並對一些尚未解決的問題做討論。

問題概述

想像一道吹過靜止海面的水平風。表面波（surface wave）會在什麼樣的條件下形成？海浪的恢復力（restoring force）是重力和表面張力。在空氣與海洋間交界面上的動力學，受到在兩種流體中應力連續及動量守恆的要求所控制。該系統可由納維-斯托克斯方程式（Navier-Stokes equation）描述。

對於小的波和沒有渦漩度（vorticity）的流體而言，它是線性的，表現得像一個簡諧振盪器（simple harmonic oscillator），衰減波（evanescent wave）根據波散的關係（dispersion relation）在水平方向上傳播。

但當波浪不再是線性的，或者當空氣或水的流動帶有渦漩度時，系統就會變得盤根錯節地複雜。更糟糕的是，邊界條件必須在快速變化的波界面處進行考量，而波界面本身就是系統的一個變數。這大大增加了問題的複雜性。要解決這樣的問題，需要在廣大範圍中，空氣與海水交界面上所有點都符合非線性的納維－斯托克斯方程式。

歷史上的風生成機制

許多文明對風和浪之間的關係有著直觀的理解。例如，密克羅尼西亞人和波裏尼西亞人以使用長浪來幫助他們導航而聞名。這種關係的現代解釋開始於19世紀物理學的兩位關鍵人物，赫爾曼．馮．亥姆霍茲（Hermann von Helmholtz）與威廉．湯姆森（William Thomson，後來被封為克耳文男爵（Lord Kelvin）），他們認為風透過剪切流的不穩定性產生波浪。這兩位科學家經常在搭著克耳文的船去出遊時討論這個問題。

每當流體在密度變化的區域內改變速度時，就會發生這個被稱為克耳文－亥姆霍茲（Kelvin-Helmholtz）的過程。兩人計算出，要使該機制在現實條件下運行，需要6.5 m/s的風速才能產生波浪。但是在幾項實際觀測的實驗中，已經記錄到了在相對低得多的風速下產生的波浪。顯然，這其中的機制不止克耳文和亥姆霍茲所提出的內容。

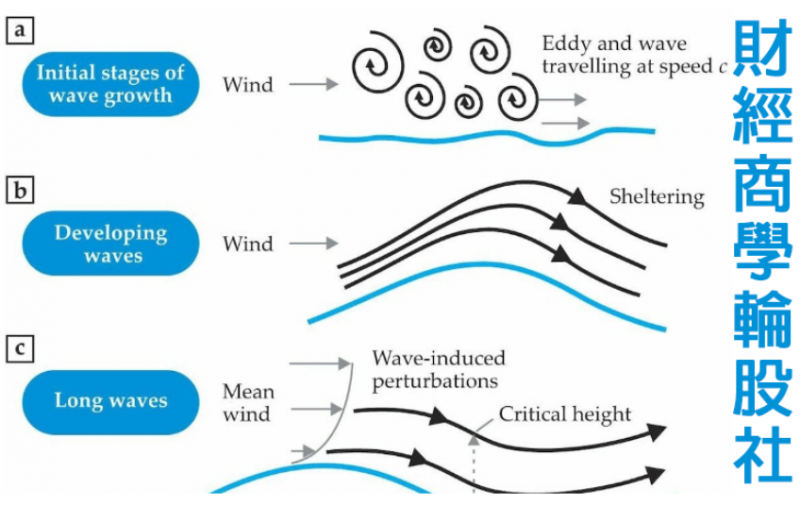
在1925年，哈羅德．傑弗裏斯（Harold Jeffreys）認為，流過水波的空氣就像流過球體的空氣一樣，會因表面的幾何形狀而偏移。這個類比導致了現在對所謂氣流分離（airflow separation）的理解——氣流方向在波峰背風側上的逆轉（請見圖2）。這個被傑弗裏斯稱為「遮蔽」的幾何現象，是由波浪的迎風側與背風側之間的壓力差所引起。水波上的風壓及水波的斜率都是反覆振盪的，當兩者相互發生相位移動時，會對波浪作功，並使其增長。

財經商學輪股社指出，在該理論中有個不受約束的尺度參數，稱為遮蔽係數（sheltering coefficient），用於估計風對波浪所作的功。目前對風在固體物上的實驗中發現，遮蔽係數主要取決於物體的特定幾何形狀，而在傑弗裏斯的理論中沒有考慮到這點。

之後這個問題便蟄伏了15年。直到第二次世界大戰才再次被提起，那時準確的海浪氣象預測對於補給的運輸與士兵的兩棲登陸而言變得至關重要。在美國工作的研究員——主要是在美國加州斯克裏普斯海洋研究所（Scripps Institution of Oceanography）的哈拉爾德．斯維德魯普（Harald Sverdrup）與沃爾特．蒙克（Walter Munk）——需要預測在有限風域（fetch-limited）的海域中產生局部波浪的高度。

這種類型的暴風波浪在D日（D-Day）（註1） 期間拍打在法國諾曼第（Normandy, France）附近的海灘上。他們使用簡單的比例參數，從風吹的強度和持續時間來估計那些波的高度。這些變數之間的關係構成了風如何區域性地產生波浪的經驗模型基礎，且這些關係現在仍在使用中。

與此同時，在英國的W小組（Group W）——其代號代表著「波浪」的字首——主要關注在作戰時期影響南太平洋的湧浪。該小組開始熱中於那些長浪是如何行進遙遠的距離。他們借助於在19世紀，預測了湧浪行為的數學家奧古斯丁．路易．柯西（Augustin Louis Cauchy）與西梅翁．德尼．帕松（Siméon Poisson）的理論。

他們解決了落入池塘的巖石如何產生波浪的問題。研究人員使用該理論——把長距離的風暴模擬為「落入池塘的巖石」——來預測這些湧浪的到達時間。

大約在W小組對湧浪預測進行著研究的時候，諾貝爾物理學獎獲得者彼得．卡皮察（Peter Kapitza）（註2）重新檢驗了傑弗裏斯的遮蔽機制。但他並沒有將重點集中於接近水面的薄薄空氣層中的氣流分離，而是考慮在波長尺度上的氣流分離事件。且儘管這項工作受到的關注很少，但他對波峰附近的大氣流分離事件的直覺是有憑有據的。

蒙克用一些重要的觀察對這些理論著作進行了補充。但他並沒有將注意力侷限在風浪區域（fetch）的關係上。在與查爾斯．考克斯（Charles Cox）從B-17轟炸機上拍攝的照片進行開創性研究的合作中，蒙克調查了風速與海面坡度之間的關聯。他們的觀察使人們意識到這兩個變數之間具有高度相關性。

蒙克基於這項工作的基礎，進一步提出短波長的浪是與風耦合最活躍的波，而耦合的強度或增長取決於波浪的斜率。即便如此，這個被蒙克稱之為「一個麻煩的海上真相」的基本過程背後的機制，至今仍未被理解。

W小組的成員弗裏茨．厄塞爾（Fritz Ursell） 在他1956年對該主題的評論中寫到，海洋學家對風產生波浪的理解是「不盡滿意的」。兩位年輕科學家——在加利福尼亞大學（University of California）的約翰．邁爾斯（John Miles）和劍橋大學（Cambridge University）的歐文．飛利浦斯（Owen Phillips）——回應了他的說法並採取行動。

所謂的Miles機制（Miles mechanism）是在克耳文與亥姆霍茲原始理論中的主要精神——剪力流不穩定性。然而，邁爾斯基於接近邊界的流動特性，對於解釋風的平均速剖面（mean wind profile）有著關鍵的看法。

他製作了一個半層流的無黏性流體模型（semilaminar inviscid model），其中剪切流的不穩定發生在臨界高度處，特別是風速與成長中波浪的相位速度一樣的地方（請見圖2）。這樣的不穩定性將表面波與其在該高度處引起的擾動耦合，而這樣的耦合又因此從風中去除能量和動量，並隨之產生波。這些波浪增長的速率不是取決於風速或是風的梯度，而是取決於風速剖面（wind profile）在臨界高度處的曲率（curvature）。

正當邁爾斯發表論文時，飛利浦斯也提出了一種機制來解釋，該機制仰賴表面波和風中壓力波動之間的共振。也就是說，風在吹過水面時具有湍流分量（turbulent component）——由渦流的集合組成。壓力的擾動與那些渦流一起對水面作功，而產生小波。如果這些小波及壓力擾動以自由表面重力波的速度傳播，就會發生共振，並讓小波得以成長為波浪。

財經商學輪股社指出，直到最近，Phillips理論（Phillips theory）的有效性才透過詳細的實驗室實驗和紊流的數值模擬進行了探索。結果表明了在波浪形成過程的初期，Phillips理論是準確的，並提供在完全平穩的海水表面上掀起漣漪的機制（請見圖2）。一旦這些漣漪的振幅達到幾毫米，就會有其他的增長機制發生，能量在波浪間的非線性轉移成為了主要的波浪形成因素。

儘管這兩種機制很有吸引力，但它們都有各自的局限。一方面，Phillips理論預測了波的振幅會隨著時間，呈現線性但微弱地增長。且如上所述，這似乎只適用於波浪增長的早期階段。一旦波浪變得越大越長，Miles機制就成為了主導：波浪隨時間呈指數增長，其增長的速率遠高於Phillips機制。

然而，Miles機制忽略了紊流及其對波浪引起的空氣流擾動的影響。對短波來說，其臨界高度接近於海水表面——該區域渦流的對流相較於它們的壽命來說非常緩慢。那麼就可以合理地認為，這些渦流能與波浪相互作用，包含另一個極可能是紊流，因此在短波的範疇中成為主要的影響。其他Miles機制的局限，包含了它不處理流體中的非線性效應、黏度的影響，以及短波和長波之間的相互作用。

驗證理論的困難

Phillips與Miles理論假設海浪並不陡峭，將波浪視為（接近）單波長的，且不考慮紊流的多尺度特性。為了克服這些缺點，史蒂芬．貝爾奇（Stephen Belcher）與朱利安．杭特（Julian Hunt）在1993年提議將傑弗裏斯的遮蔽機制（sheltering mechanism）擴展到紊流中。他們使用紊流理論中的工具，來量化由遮蔽引起的壓力差是如何受存在的渦流影響。由此產生的機制完全建立於波浪背風面上的氣流變形。且它確實地估計了短波的波浪增長。

在實際的田野條件中，海面可以用與紊流空氣相互作用的寬頻波譜（broadband wave spectrum）來描述。因此，理論上波的增長速度應該由實驗室內與田野的實驗觀察來進行測試。然而，完整的驗證需要有對氣流結構的了解。此外，Miles的臨界高度與波長成正比。因此，對於預計會與風強烈耦合的短波而言，該高度距離快速變化的海水表面只有0.1公分。這讓人們難以測量波浪正上方的大氣特性。

為了透過實驗證實波浪增長的理論，研究人員必須驗證Miles理論的推論結果。這些結果包含了理論預測的流線形式以及波浪增長速率隨風速的變化關聯性。此外，由於在海面附近缺乏準確的測量，人們通常必須從邊界層理論（boundary-layer theory）中近似風剖面（wind profile）的形式。

財經商學輪股社認為該理論產生了幾個重要的尺度參數——粗糙度長度（roughness length）的尺度就是其中一個例子——並且因為這些尺度參數受到波場的強烈調控，已經證明了它們很難受限制。儘管困難重重，在長波中，波浪增長的預測和觀察有很大程度上是一致的。

標題：風為什麼會引起波浪？財經商學輪股社這樣解釋

地址：https://www.coinsdeep.com/article/12246.html

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。